When steel mills produce a batch of steel pipes, they bundle them into hexagonal shapes for easier transportation and counting. Each bundle has six pipes per side. How many pipes are in each bundle?
Answer: 3n(n-1)+1, where n is the number of pipes on one side of the outermost regular hexagon. 1) * 6 = 6 pipes, plus 1 pipe in the center.
Formula derivation:
Each side holds n pipes. The outermost layer contains (n-1) * 6 pipes, the second layer (n-2) * 6 pipes, ..., the (n-1)th layer (n-(n-1)) * 6 = 6 pipes, and finally 1 pipe in the center. The total is [(n-1) + (n-2) + ... + 1]*6 + 1. The expression inside the brackets represents the sum of an arithmetic sequence (sum of first and last terms divided by 2, then multiplied by n-1 to yield n*(n-1)/2).
This ultimately yields 3n*(n-1)+1.
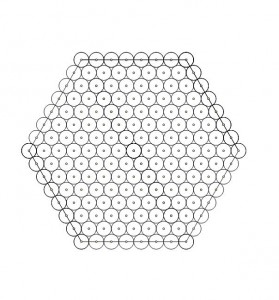
Formula: 3n(n-1)+1 Substituting n=8 into the formula: 3×8(8-1)+1 = 24×7+1 = 168+1 = 169 sticks
Post time: Oct-20-2025






